Skewness and kurtosis

Skewness:

Average value, dispersion, and shape are the three ways that a frequency distribution can vary. Skewness and kurtosis distinguish frequency distributions based on shape from each other. It is possible for two distributions with identical mean and standard deviation values to have distinct shapes. To differentiate between various distribution types, one uses the skewness metric. The absence of symmetry in a distribution is referred to as skewness. The balance of the distribution is pushed to one side in an asymmetric distribution because the mean and median fall at separate places. Skewed distribution refers to an unbalanced distribution.

• Symmetrical Distribution: It is a sort of distribution where the mean, median, and mode values are all equal.
• Asymmetrical Distribution: Skewed distributions are neither symmetrical nor asymmetrical distributions. Based on the mean and mode values, it might be one of the two types that are favorably or negatively skewed. The following is a list of them:
  • Positively Skewed Distribution: This sort of distribution has a mean value that is maximum and a mode value that is minimum. According to the figure below, the median is situated between the two.
  • Negatively Skewed Distribution: Distributions that are negatively skewed have maximum values for the mode and minimum values for the mean. According to the figure below, the median is situated between the two.

Test Of Skewness

The following tests can be used to determine whether or not a distribution is skewed:

• The mean, median, and mode numbers must not be same.
• The data shouldn't display a bell-shaped distribution when plotted on a graph.
• It is not expected that the sum of the positive and negative departures from the median will be equal.
• The quartiles do not lie equally from the median.
• At locations where the mode's divergence from it is equal, frequencies are not distributed equally.

Measure Of Skewness

The skewness typically ranges from -1 to +1. The skewness metrics are:

• Karl Pearson's measure,
• Bowley’s measure,
• Kelly’s measure, and
• Moment’s measure.

These measures are discussed briefly below:

Karl Pearson's Measure:

The formula for measuring skewness as given by Karl Pearson is as follows:
Skewness = Mean - Mode
Coefficient of skewness=\frac{mean-mode}{standard\;deviation}

When the mode is unknown it is calculated as:

Coefficient of skewness=\frac{mean-(3median-3mean)}{standard\;deviation}

Coefficient of skewness=\frac{3(mean-median)}{standard\;deviation}

Coefficient of skewness is also denoted as Skp.

Example 1:

Given the following data, calculate the Karl Pearson's coefficient of skewness: ∑x = 452 ∑x2= 24270 Mode = 43.7 and N = 10

Solution:

Coefficient\;of \;skewness=\frac{mean-mode}{standard\;deviation}

mean\overline{(x)}=\frac{\sum{X}}{N}

=45.2

SD=\sqrt{\frac{\sum{x^2}}{N}-(\frac{\sum{x}}{n})^2}

=19.59

So using the formula,

Skp=\(\frac{mean-mode}{SD}\)

=\(\frac{45.2-43.7}{19.59}\)

=0.08

This shows that there is positive skewness in the above example.

Bowley's Measure:

Bowley provided the equation to calculate the skewness of the quartile-based frequency distribution. The skewness formula is as follows:

skewness=\frac{Q3+Q1-M}{Q3-Q1}$$ where Q1 and Q3 are 1st and 3rd quartiles and M is a median.

Kelly's Measure:

Kelly provided the percentile-based skewness measure. The following equation can be used to calculate skewness:

Coefficient Of Skewness=\frac{P90-2P50-P10}{P90-P10}

Where P represents the percentile. With this approach, we can calculate skewness by first determining the respective percentiles. Typically, this approach is not applied.

Moments Measure:

Moments is another metric for skewness and is represented by the symbol. Following are the first four instances of mean or center moments:

• First Moment=
  • µ1=\frac{1}{N}\sum(x1-\overline{x})
• Second Moment=
  • µ2=\frac{1}{N}\sum(x1-\overline{x})^2
• Third Moment=
  • µ3=\frac{1}{N}\sum(x1-\overline{x})^3
• Fourth Moment=
  • µ4=\frac{1}{N}\sum(x1-\overline{x})^4

These moments are used for individual items, in the case of frequency distribution moments are represented as follows:

First Moment=µ1=\frac{1}{N}\sum{fi}(x1-\overline{x})

Here,frequency is included. Similarly it can be included to calculate moments in other cases too.

It may be noted that the first central moment is zero, that is, μ= 0. The second central moment is μ2= σ , indicating the variance. The third central moment μ3 is used to measure skewness. The fourth central moment gives an idea about the Kurtosis.

Kurtosis:

Kurtosis can also be used to determine how a frequency curve is shaped. Kurtosis, which meaning bulginess, is a Greek term. Kurtosis describes a frequency distribution's degree of peakedness, whereas skewness indicates how lopsided the distribution is. Based on the design of their peaks, Karl Pearson divided curves into three groups. Mesokurtic, leptokurtic, and platykurtic are these. The image below displays these three different kinds of curves:

The figure shows that the mesokurtic curve is not very flat or overly rounded. While the platykurtic curve is flat, the leptokurtic curve is more pronounced. According to Karl Pearson, the coefficient of kurtosis is β2= μ4/ μ22. The value of β2=3 applies to a normal distribution, or mesokurtic curve. The curve is known as a leptokurtic curve and is more pronounced than the usual curve if β2 turns out to be > 3. The curve is known as a platykurtic curve and is less peaked than the usual curve when β2 < 3 once more.

Example 2:

Calculate the kurtosis if μ4=42.1312 andμ2=6.4.

Solution:

As we know,

β2= μ4/ μ22

=1.03

which is <3 so the distribution is platykurtic.

Kurtosis measurement is highly beneficial in choosing the right average. As an illustration, the mean is best for a normal distribution, the median is best for a leptokurtic distribution, and the quartile range is best for a platykurtic distribution.

The following formula can be used to calculate Kurtosis based on quartiles and percentiles:

K=\frac{Q}{P90-P10}

Where K = kurtosis, Q = ½ (Q3 – Q1) is the semi-interquartile range; P90 is 90th percentile and P10 is the 10th percentile. This is also known as the percentile coefficient of kurtosis. In the case of the normal distribution, the value of K is 0.263.

Box and Whisker Plots:

The display of statistical data on a plot is called a box-whisker plot. It is made up of the box, which symbolizes the center pair of data points. We must first arrange the data and get the median before we can discover the box and whisker graphic. The median splits the data in half, and we then determine the median for each half. They are referred to as Q1, Q2, and Q3.

Example 3:

Draw a box-and-whisker plot for the following data set:

4.3, 5.1, 3.9, 4.5, 4.4, 4.9, 5.0, 4.7, 4.1, 4.6, 4.4, 4.3, 4.8, 4.4, 4.2, 4.5, 4.4

Arranging the data in ascending order,

3.9, 4.1, 4.2, 4.3, 4.3, 4.4, 4.4, 4.4, 4.4, 4.5, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1

Then we calculate the median for the data since there are 17 items median is the 9th data.i,e.

3.9, 4.1, 4.2, 4.3, 4.3, 4.4, 4.4, 4.4, 4.4, 4.5, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1

The median is Q2 = 4.4.

Again the median divides the data into two halves we find the median of each half

3.9, 4.1, 4.2, 4.3, 4.3, 4.4, 4.4, 4.4and 4.5, 4.5, 4.6, 4.7, 4.8, 4.9, 5.0, 5.1

The first half has eight values, so the median is the average of the middle two:

Q1 = (4.3 + 4.3)/2 = 4.3

The median of the second half is:

Q3 = (4.7 + 4.8)/2 = 4.75

Box and whisker plot is represented as follows:

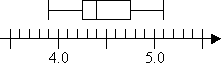
Where,

min=3.9

Q1=4.3

Q2=4.4

Q3=4.75

max=5.1

Reference

• Kunda, Surinder. An Introduciton to business statistics. n.d.
• purplemath.com/modules/boxwhisk.htm