Gravity
Subject: Science

Overview
The force that pulls neighboring objects toward the cores of other planets and satellites, as well as Earth, is known as gravity. According to Newton's universal law of gravitation, the force of gravity gradually diminishes and vanishes as a planet rises in altitude. When an object falls freely, it experiences acceleration from gravity. When air resistance is minimal, this acceleration is 9.8 m/s. According to Aristotle's rules of motion, heavier objects fall before lighter ones, but Galileo's experiment showed that gravity accelerates all freely falling bodies equally. When the cylinder was turned upside down in the feather and coin experiment, the coin fell more quickly than the feather, while the feather fell more slowly because of air resistance. The acceleration that gravity causes depends on the planet's mass and squared radius. Because of its equatorial and polar regions, the Earth accelerates more rapidly near the poles. The average acceleration due to gravity is 9.81 m/s2, with a decrease in velocity at the maximum before returning to Earth.
Gravity
Nearby objects are being drawn towards the cores of Earth and other planets and satellites. The force of gravity is the name given to the force that neighboring objects get from the planet or satellite. It is sometimes referred to as the object's weight. Newton's universal law of gravitation states that as a planet gets higher, the force of gravity weakens and eventually disappears. Since Earth has a distinct gravitational field, so do other planets and satellites.
In our daily lives, we witness the impact of Earth's gravity in various ways. The following list includes a few of these effects:
- Because of gravity, everything has weight.
- The atmosphere envelops Earth because of gravity.
- The gravitational pull of the Earth causes objects dropped from a certain height to fall toward its center.
- Water in rivers and streams flows downward as a result of gravity.
- A falling item accelerates due to the force of gravity.
Acceleration Due to Gravity
Calculation of Acceleration Due to Gravity
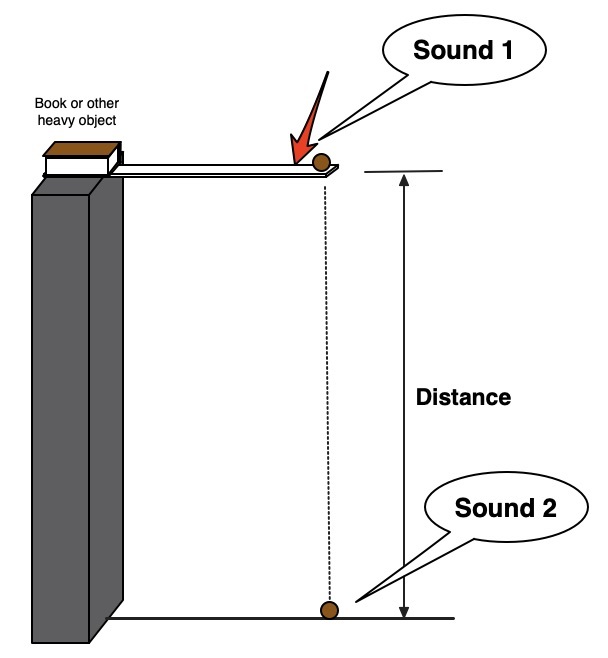
Grab a stopwatch and a little stone. Drop the stone from varying heights, such as a building's first and second floors. Simply remove the stone from your hand by releasing your fingers, and drop the stone so that your fingers are not pressing down on it. Tell a buddy to time how long it takes the stone to touch down with a stopwatch.
Equations of motion and the resulting data (h = ut+\(\frac12\)at2, v2 = u2 + 2 ah) When the stone strikes the ground, use v to determine its acceleration and ultimate velocity. Consider the stone's starting velocity while performing the calculation. (u) = 0.
A table like the one below can be used for data collection and necessary calculations.
| Data collection | h | t |
a=\(\frac {2h}{t^2}\)
|
Average acceleration | v= \(\sqrt{(2ah)}\) | result |
| first time | ........ | ....... | a1=... | = \(\frac{a^{1}+a^{2}+a^{3}}{3}\) | V1= \(\sqrt{(2ah_{1})}\) | ..... |
| second time | ........ | ....... | a2=.... | ............................. | V3= \(\sqrt{(2ah_{2})}\) | ..... |
| third time | ........ | ....... | ..... | V3= \(\\sqrt{(2ah_{2})}\) | ..... |
The object released from the hand is set in motion due to the earth's gravity, and it acts constantly throughout the motion. The more the object falls, the faster its velocity will be. Increasing the velocity of the object means it is accelerating. Thus, acceleration is produced in the body as it falls freely towards the earth's surface because of gravity. The acceleration of a falling stone is 9.8 m/s when the air resistance is negligible, i.e., almost zero. Such acceleration is due to the gravity of the earth. The acceleration produced in a freely falling object due to the force of gravity is called acceleration due to gravity. It is denoted by 'g and the SI unit is meter per second squared (m/s2).
In this exercise, the paper ball and the stone with different masses fall together, but the paper ball and the sheet of paper fall at different speeds. Consequently, the mass of an item falling towards the earth's surface has no bearing on the rate at which its velocity changes. A sheet of paper falling in the air experiences an upward push from the air resistance, which causes its velocity to decrease. However, there isn't much air resistance in the case of a paper ball and stone, so gravity is the only force driving their combined fall toward the earth's core.
The moon's surface lacks an atmosphere, so everything falls freely and without hindrance. All things fall with the same accelerative force in such a scenario because of gravity.
Aristotle, who was born in Greece in 384 BC, developed the principles of motion, which state that heavier things fall before lighter ones. Galileo's experiment from the seventeenth century demonstrated this law to be false. Galileo discovered that both balls touched the ground simultaneously when he dropped two balls simultaneously from the Leaning Tower of Pisa in Italy in the year 1590 BC. He came to the conclusion that gravity causes the same acceleration for all freely falling bodies. The feather-and-coin experiment later provided evidence for this.
Feather and Coin Experiment
A vacuum pump and a glass cylinder are linked in Figure. At the bottom are a penny and a feather.  The coin falls more quickly than the feather when the cylinder is flipped upside down and air is present within.The coin and the feather are observed to fall together if the cylinder is tipped upside down and the air is pushed out using the vacuum pump.
The coin falls more quickly than the feather when the cylinder is flipped upside down and air is present within.The coin and the feather are observed to fall together if the cylinder is tipped upside down and the air is pushed out using the vacuum pump.
The air resistance within the cylinder is the reason why the coin and feather did not fall together the first time. Because the feather has a larger surface area than the coin, there is more air resistance acting on it than there is on the coin, which slows acceleration. The feather thus descends more slowly than the coin. The feather and the coin fall together the second time because there is no air within the cylinder, or air resistance. All objects experience the same acceleration owing to gravity when there is no air resistance. In other words, the mass of the falling body has no bearing on the magnitude of 'g'.
Calculation of Acceleration Due to Gravity
Assume a planet with mass 'M' and radius 'R' has a body of mass'm' on its surface. The gravitational force generated between them is if the planet's gravity pulling on the body is F.
F= \(\frac{GMm}{R^2}\)
If this force produces acceleration 'g' in mass 'm', then from the Second law of motion,
F= mg ....... (ii)
From the equations (i) and (ii),
mg= \(\frac{GMm}{R^2}\)
g= \(\frac{GM}{R^2}\)
According to equation (iii), the acceleration depends only on the mass M' and radius 'R' of the planet.
The fact that the equation does not take into account the mass of the falling item verifies that, while falling freely, all masses accelerate at the same rate, which is consistent with the findings of Galileo's activities and the feather-coin experiment. The position of a planet or satellite, such as Earth, affects the radius 'R' value, which is not constant. G and M in equation (iii) are both constants.
In this instance, the acceleration brought on by gravity is inversely related to the planet's or satellite's radius squared. Hence, g α \(\frac 1{R^2}\)
Gravitational acceleration is a function of the planet's or satellite's radius and mass. For instance, although Jupiter has a mass around 319 times that of Earth, its acceleration is just 2.6 times that of Earth's gravity. The primary factor in this is Jupiter's radius. Jupiter's radius is 11 times larger than Earth's. Despite Jupiter's massive mass, the net effect on the acceleration due to gravity will be just \(\frac{319}{121}\) = 2.6 times larger because the acceleration due to gravity is inversely proportional to the square of the radius.
On substituting the mass of the earth as 5.972 x1024 and the radius as 6371 km in equation (iii),
g= \(\frac{6.67×10^{-11}×5.972×10^{24}}{(6.371×10^{6})^{2}}\)
Since R's value varies around the world, it follows that gravity's acceleration does as well.
Variation in Acceleration Due to Gravity of the Earth
The earth is not circular in every way. It has a little bulge in the equatorial area and is somewhat flattened at the poles.As a result, the Earth's radius is greater at the equator and less at the poles, as seen in Figure. Because gravity is inversely proportional to the square of the earth's radius, its acceleration is greater near the poles than at the equator. 'G' has a value of 9.78 m/s2 in the equatorial zone and 9.83 m/s2 in the polar region. In the polar zone, things fall more quickly than in the equatorial region due to the greater value of 'g' in that location.
On Earth, the average value of 'g' is thought to be 9.81m/s2. This indicates that a body falling freely would accelerate by 9.81 meters per second toward the earth's surface. On the other hand, a body propelled upward vertically has a 9.81 meter per second drop in velocity. At the highest point it covers, the velocity drops to zero before returning to Earth.
Things to remember
- Gravity is the force that draws nearby objects towards Earth's cores and other planets and satellites.
- Newton's universal law of gravitation states that as a planet gets higher, the force of gravity weakens and eventually disappears.
- Acceleration due to gravity is the acceleration produced in a freely falling object due to the force of gravity.
- The Feather and Coin Experiment involves a vacuum pump and a glass cylinder with a penny and a feather at the bottom. The coin falls more quickly when the cylinder is flipped upside down and air is present, while the feather falls more slowly due to air resistance. All objects experience the same acceleration due to gravity when there is no air resistance.
© 2021 Saralmind. All Rights Reserved.


 Login with google
Login with google