Unit
Subject: Science

Overview
Physical quantities are measured using two categories: fundamental units and derived units. Fundamental units exist independently and cannot be reduced to simpler forms. Derived units are made up of two or more fundamental units and do not exist on their own. Analyzing unit-wise equations helps verify the consistency and validity of these formulas and equations. Units on both sides of an equation must match for it to be valid. Physical quantities can be added or subtracted as long as their fundamental unit composition remains the same. Unit analysis is necessary to show the accuracy of an equation, understand how two physical quantities are related, and change units from one measurement system to another.
Units are used to measure physical quantities. There are two categories into which all physical quantities' units fall:
- Fundamental unit
- Derived unit
Fundamental Unit
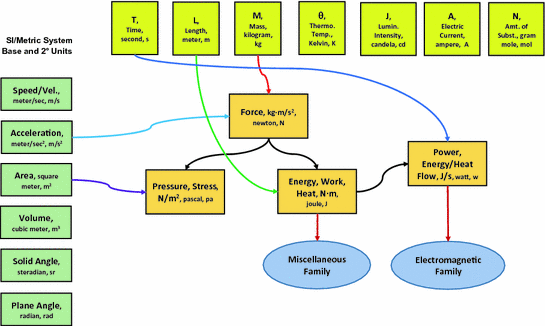
The term "fundamental unit" refers to a unit of measurement that exists independently, is not dependent on other units, and cannot be reduced to any simpler form. For instance, the kilogram is the fundamental unit of mass, the second is the fundamental unit of time, and the meter is the fundamental unit of length. The following is a list of the seven fundamental units in the SI system:
| S.No. | Physical Quantity | Fundamental Unit | Symbol |
| 1. | Length | meter | m |
| 2. | Mass | kilogram | kg |
| 3. | Time | second | s |
| 4. | Temperature | kelvin | k |
| 5. | Luminous intensity | candela | cd |
| 6. | Electric Current | ampere | A |
| 7. | Amount of substance | mole | mol |
Derived Unit
A derived unit of measurement is a unit of measurement that is made up of two or more fundamental units and does not exist on its own. Density, for instance, is measured in kg/m3. There are two basic units that make up this system: kilograms and meters. Similar to this, the unit of force is kgms, where the three basic units that make up this unit are kilogram (kg), meter (m), and second (s). Since it is challenging to pronounce kgms in everyday speech, this combined form of units is known by its simpler name, newton (N). Consequently, N = kgms-2. Pascal (Pa) is also the unit of pressure. The unit of measurement is kgm 1s-2. This gives specific names to units of many derived quantities.However, for some physical quantities, such as density, which has a unit of kgm-3, a combination of fundamental units is used.There's no easier way to call it.
| Quantity | Formula | Combination of Base Units According to the Formula | Fundamental Units | Derived Units |
| Area | l × b | meter × meter | m2 | m2 |
| Volume | l × b × h | meter × meter × meter | m3 | m3 |
| Density |
\(\frac {mass}{volume}\) |
\(\frac {kilogram}{meter^3}\) |
kg/m3 | kg/m3 |
| Velocity |
\(\frac {displacement}{time}\) |
\(\frac {meter}{second}\) |
m/s | m/s |
| Acceleration |
\(\frac {velocity}{time}\) |
\(\frac {meter}{second^2}\) |
m/s2 | m/s2 |
| Force | mass × acceleration | \(\frac {kilogram\:×\:meter}{second^2}\) | kgm/s2 | Newton (N) |
| Pressure |
\(\frac {force}{area}\) |
\(\frac {(kgm/s^2)} {meter^2}\) |
kg/ms2 | Pascal (P) |
| Work | force × distance | \(\frac {kgm/s^2} {meter}\) | kgm2/s2 | Joule (J) |
| Power |
\(\frac {work}{time}\) |
\(\frac {kgm^2/s^2}{second}\) |
kgm2/s3 | Watt (W) |
| Moment | force × distance | (kgm/s2) × meter | kgm2/s2 | Nm |
| Frequency |
\(\frac {1}{time}\) |
\(\frac {1}{s}\) |
s-1 | Hz |
Based on how the physical quantity is defined, analysis can be done to find out what the derived unit, which includes the fundamental units, is made of. For instance:
- The unit of area is a square metre
Analysis: Area = length x breadth = m x m = m2
Therefore, the unit of area is m2. This unit is formed from two fundamental units.
- The unit of force is Newton (N)
Analysis: F = ma is the definition of force.
The acceleration (a) unit is ms-2, and the mass (m) unit is kg. Consequently, N kgms-2. Therefore, the fundamental units of kilogram, meter, and second combine to form the newton, which is the unit of force.
Analysis of Unit-Wise Equation
Numerous equations and formulas can be found at the end of scientific research studies. The examination of the units used in these physical quantities allows one to verify the consistency and validity of these formulas and equations. Units on both sides of an equation must match for the equation to be validated. Using the equation s = v x t as an example, the fundamental units of the quantities on the left and right sides of the equation are m and t, respectively, and when performing the unit analysis of the equation, it is also ms-1 x s = m. Therefore, this equation is valid.
However, in the event that someone asserts that s = \(\frac vt\), the unit analysis reveals that the fundamental unit of the quantity on the left is m, while the fundamental unit of the quantity on the right is either ms-1/s or ms-2. Thus, the physical quantity unit on the left side of the equation does not equal the physical quantity unit on the right. Thus, the equation \(\frac vt\) is wrong or invalid.
Physical quantities can be added to or subtracted, as long as their fundamental unit composition remains the same. For instance, u+v is conceivable since they both use the same unit, ms-1. In a similar vein, s - at2 is also feasible since, when simplified, the fundamental units of s and at2 are both m. However, s + at is not possible because the unit of s, i.e., distance covered, is m and the fundamental unit of at is ms-1. Because of this, they cannot be added because the basic units' compositions differ.
Example: Use unit analysis to verify the accuracy of the equation below.
v2 = u2 + 2as
s = ut + \(\frac12\)a2t
Now,
v2 = u2 + 2as ⇒ m2s-2 + m2s-2
In the above equation, there is uniformity in the unit of physical quantity on either side. So, this is a valid equation.
s = ut + \(\frac 12\) a2t
m = ms-2 x s + (ms-2)2 X s
m = m + m2s-3
The base units of the physical quantities on either side of the equation above are not similar. Therefore, this equation is unsound.
Unit analysis is needed to show that an equation is correct, figure out how two physical quantities are related, and change units from one measurement system to another.
Things to remember
- The validity and consistency of these formulas and equations can be confirmed by looking at the units used in these physical quantities.
- The fundamental units of kilogram, meter, and second combine to form the newton, the unit of force.
- To prove an equation's correctness, ascertain the relationship between physical quantities, and convert units between various measurement systems, unit analysis is required.
© 2021 Saralmind. All Rights Reserved.

 Login with google
Login with google