Lens
Subject: Science

Overview
A lens is a transparent medium with at least one spherical surface that refracts light rays to either diverge or converge at a single point. There are two main types of lenses: convex and concave. Convex lenses have a greater thickness in the center than the edges and are used in various devices like projectors, cameras, microscopes, and eyeglasses. Concave lenses have a thinner middle section and are used to diverge light beams. The lens's curvature affects the ray diagrams of images created, with guidelines for creating ray diagrams for light rays diverged by a concave lens and converged by a convex lens.
A hand lens's glass or plastic form has a spherical surface as well. Light rays that pass through these kinds of surfaces refract light, which causes them to either diverge or converge at a single point.
Putting water between the two circular plastic surfaces creates a lens. It is a lens that refracts light. When light passes through this lens, objects appear larger than they are. The lens and the spherical mirror have some similar properties. A convex lens and a concave mirror are shown as being made from a spherical glass ball. Similar to this, adding water between the two circular surfaces creates a sample lens. Even when water is poured into one of the circular pieces of the bottle, it will refract light. It appears to have been made from two solid, spherical portions. Therefore, a lens is a transparent medium that has at least one spherical surface.
Types of Lenses
There are primarily two kinds of lenses. Convex and concave lenses are what they are. A convex lens is one that has a greater thickness in the center than the edges. Convex lenses are also known as converging lenses because they have the ability to converge light beams. In gadgets like projectors, cameras, microscopes, and eyeglasses, among others, convex lenses are employed. Our eyes also have naturally occurring convex lenses. A concave lens is one that has a thinner middle section than its borders. Because of its capacity to diverge light beams, the concave lens is also known as a diverging lens.
Terminologies Related to the Lens
- Center of Curvature
The center of the sphere that creates the curved portion of the lens is known as the center of curvature. Most lenses have two centers of curvature, typically denoted C1 and C2, because they are composed of two spherically curved surfaces.
- Radius of Curvature
The distance between the lens's surface and the center of curvature is known as the radius of curvature. R is used to represent it in a ray diagram.
- Optical Center
The geometrical center of the lens, where the major axis crosses the lens surface, is known as the optical center. O is used to represent it in a ray diagram.
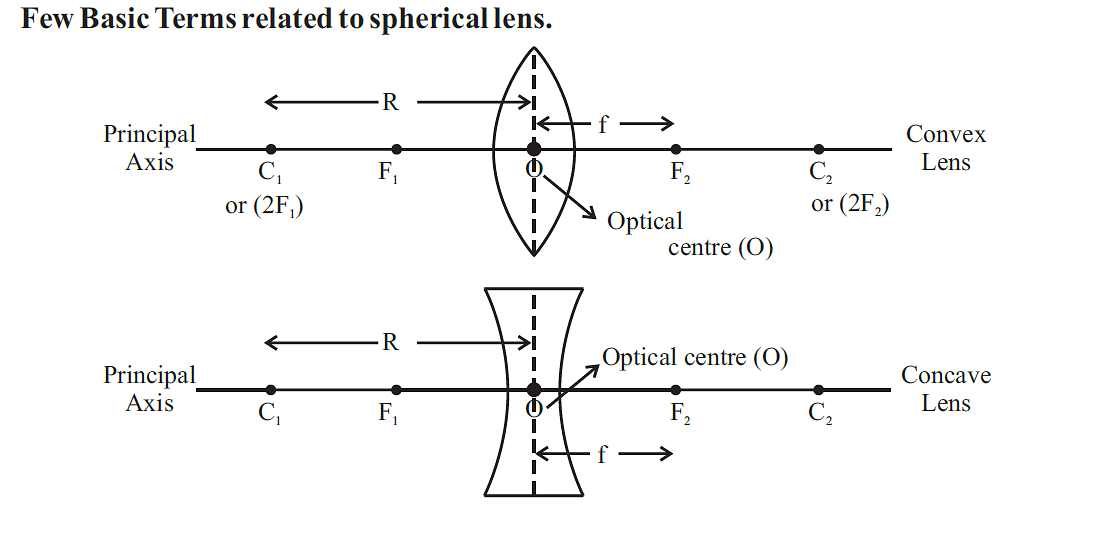
- Principal Axis
The line that runs across the lens's two centers of curvature and optical center is known as the principle axis. The lens is split into two symmetric halves.
- Principal Focus
A convex lens is considered a mixture of prisms. On the upper half of the convex lens, the bases of the prisms face downwards and on the lower half, the bases of the prisms face upwards. Every time a ray emerges from the prism, it is bent toward the direction of the base. The prisms in the center of the lens refract the light more than those on the edges and the rays passing through the principal axis pass in a straight line without any deviation. As a result of this, rays that are traveling parallel to the principal axis converge at a point on the principal axis after passing through the lens. The diagram's letter F stands for that location, which is known as the convex lens' principal focus.

 The principal focus is the point on the principal axis from where the light rays traveling parallel to the principal axis converge or appear to converge after passing through the lens.
The principal focus is the point on the principal axis from where the light rays traveling parallel to the principal axis converge or appear to converge after passing through the lens.
- Focus Distance
The focal length measures how far the lens's focus (F) is from its optical center (O). The symbol for it is f. Two times the focal length is the radius of curvature.
Rules to Draw Image Formed by a Convex Lens
The curvature of lenses affects the ray diagrams of the images they create. The following guidelines apply for creating the ray diagrams for light rays that are diverged by a concave lens and converged by a convex lens:
- Light beams do not bend as they pass past the lens's optical center. They make no stops in their forward motion.
- The light beams parallel to the principal axis converge and pass through the focus. The same rays appear to diverge from the focus when they go through a concave lens.
- Following refraction in the lens, light beams that go through the focus of the lens emerge parallel to the primary axis.
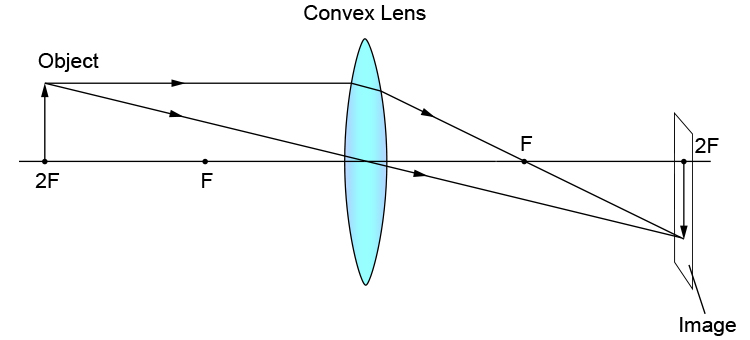
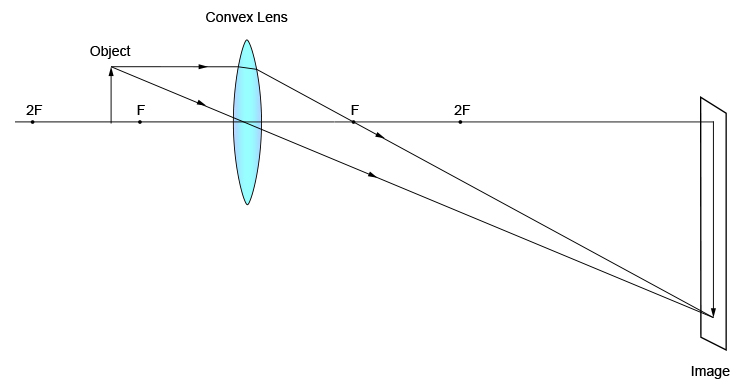
Image Formed by a Convex Lens
Consider a convex lens with a known focal length. Place the lens such that at least two focal lengths (f) remain on either side of it when it is positioned in the center of the ruler. Now, position a candle in different places along one side of the lens. For each position of the candle, put the screen on the opposite side and move it forward and backward until a clear image of the candle is formed on the screen. Observe the characteristics of the image. The object's position with respect to the optical center O determines the properties of the image that a convex lens forms. The images formed by placing an object at different positions in front of the convex lens are shown in the diagram and their characteristics are presented in the table.
The size of the image continuously grows during image formation while the item is kept closer to the convex lens, and vice versa.
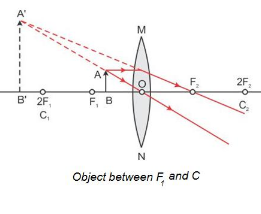
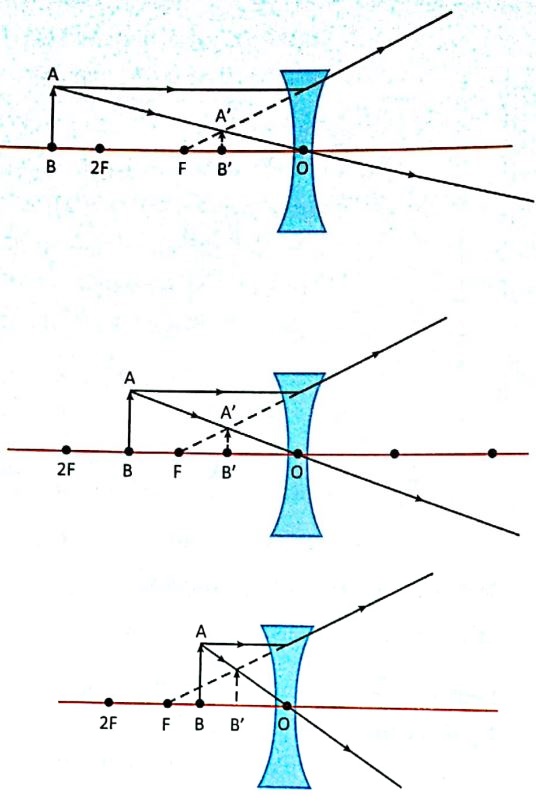
Image Formed by a Concave Lens
After refraction, light beams traveling through a concave lens migrate away from the primary axis and never physically cross paths. A virtual image is formed at the place where the refracted rays are cut if they are generated in the other direction. As a result, any point on an object in front of a concave lens will appear virtual, erect, and shrunk. The lens in a door peephole creates this kind of image.
Power of a Lens
When light beams refract via a lens, a thicker lens with a larger curvature will have a greater degree of refraction than a narrow lens with a smaller curvature. The power of a lens refers to its capacity to converge or diverge light beams.
A convex lens's focal length is shorter but its capacity to converge light rays is better if it has a bigger curvature and thickness and converges parallel light rays closer to its optical center (0). In a similar vein, a concave lens with a shorter focal length can diverge light rays more effectively. As a result, a lens's focal length (f) determines its power. The power of a lens is defined as the reciprocal of its focal length in meters, expressed mathematically:
Lens Power (P) = \(\frac {1}{f (in meter)}\)
The diopter is the SI unit of power. D indicates this. The power of a convex lens with a positive focal length is also positive. A concave lens with a negative focal length also has negative power.
The curvature of glass lenses remains constant. It doesn't alter by itself. However, as we look at close-up or far-off objects, the convex lens in our eyes can change in curvature, which alters the power of the lens.
Things to remember
- A lens is a transparent medium with at least one spherical surface, which refracts light rays and causes them to either diverge or converge at a single point.
- There are two main types of lenses: convex and concave.
- Convex lenses have a greater thickness in the center than the edges and are used in various devices like projectors, cameras, microscopes, and eyeglasses.
- Concave lenses have a thinner middle section than their borders and are also known as diverging lenses.
- The optical center is the geometrical center of the lens, and the principal axis is the line that runs across the lens's two centers of curvature and optical center.
- The ability of a lens to converge or diverge light beams is what determines its power.
- A convex lens's focal length (f) determines its power, which is defined as the reciprocal of its focal length in meters.
© 2021 Saralmind. All Rights Reserved.





 Login with google
Login with google